How To Build a Naive Bayes Classifier
In machine learning a classifier is able to predict, given an input, a probability distribution over a set of categories. Some use-cases for building a classifier:
- Spam detection, for example you could build your own Akismet API
- Automatic assignment of categories to a set of items
- Automatic detection of the primary language (e.g. Google Translate)
- Sentiment analysis, which in simple terms refers to discovering if an opinion is about love or hate about a certain topic
In general you can do a lot better with more specialized techniques, however the Naive Bayes classifier is general-purpose, simple to implement and good-enough for most applications. And while other algorithms give better accuracy, in general I discovered that having better data in combination with an algorithm that you can tweak does give better results for less effort.
In this article I’m describing the math behind it. Don’t fear the math, as this is simple enough that a high schooler understands. And even though there are a lot of libraries out there that already do this, you’re far better off for understanding the concept behind it, otherwise you won’t be able to tweak the implementation in response to your needs.
0. The Source Code #
I published the source-code associated at github.com/alexandru/stuff-classifier. The implementation itself is at lib/bayes.rb, with the corresponding test/test_003_naive_bayes.rb.
1. Introduction to Probabilities #
Let’s start by refreshing forgotten knowledge. Again, this is very basic stuff, but if you can’t follow the theory here, you can always go to the probabilities section on khanacademy.org.
1.1. Events and Event Types #
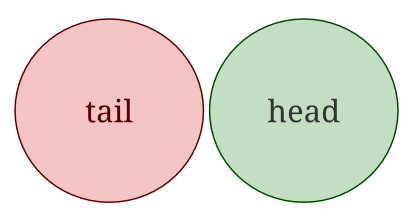
An “event” is a set of outcomes (a subset of all possible outcomes) with a probability attached. So when flipping a coin, we can have one of these 2 events happening: tail or head. Each of them has a probability of 50%. Using a Venn diagram, this would look like this:
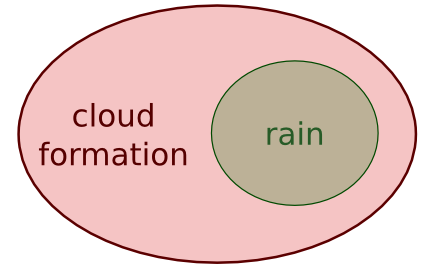
And another example which clearly shows the dependence between “rain” and “cloud formation”, as raining can only happen if there are clouds:
The relationship between events is very important, as you’ll see next:
- 2 events are disjoint (exclusive) if they can’t happen at the same time (a single coin flip cannot yield a tail and a head at the same time). For Bayes classification, we are not concerned with disjoint events.
- 2 events are independent when they can happen at the same time, but the occurrence of one event does not make the occurrence of another more or less probable. For example the second coin-flip you make is not affected by the outcome of the first coin-flip.
- 2 events are dependent if the outcome of one affects the other. In the example above, clearly it cannot rain without a cloud formation. Also, in a horse race, some horses have better performance on rainy days.
What we are concerned here is the difference between dependent and independent events, because calculating the intersection (both happening at the same time) depends on it. So for independent events, calculating the intersection is easy:
Some examples:
- if you have 2 hard-drives, each of them having a 0.3 (30%) probability of failure within the next year, that means there’s a 0.09 (9%) probability of them failing both within the next year
- if you flip a coin 4 times, there’s a 0.0625 probability of getting a tail 4 times in a row (0.5 ^ 4)
Things are not so simple for dependent events, which is where the Bayes Theorem comes into play.
1.2. Conditional Probabilities and The Bayes Theorem #
Let’s take one example. So we have the following stats:
- 30 emails out of a total of 74 are spam messages
- 51 emails out of those 74 contain the word “penis”
- 20 emails containing the word “penis” have been marked as spam
So the question is: what is the probability that the latest received email is a spam message, given that it contains the word “penis”?
So these 2 events are clearly dependent, which is why you must use the simple form of the Bayes Theorem:
Or visually:
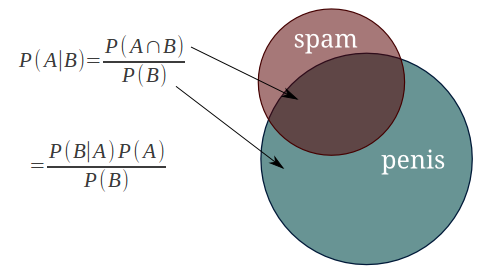
With the solution being:
This was a simple one, you could definitely see the result without complicating yourself with the Bayes formula.
1.3. The Naive Bayes Approach #
Let us complicate the problem above by adding to it:
- 25 emails out of the total contain the word “viagra”
- 24 emails out of those have been marked as spam
- so what’s the probability that an email is spam, given that it contains both “viagra” and “penis”?
Shit just got more complicated, because now the formula is this one:
And you definitely don’t want to bother with it if we keep adding words. But what if we simplified our assumptions and just say that the occurrence of penis is totally independent from the occurrence of viagra? Then the formula just got much simpler:
To classify an email as spam, you’ll have to calculate the conditional probability by taking hints from the words contained. And the Naive Bayes approach is exactly what I described above: we make the assumption that the occurrence of one word is totally unrelated to the occurrence of another, to simplify the processing and complexity involved.
This does highlight the flaw of this method of classification, because clearly those 2 events we’ve picked (viagra and penis) are correlated and our assumption is wrong. But this just means our results will be less accurate.
2. Implementation #
I mention it again, you can take a look at the source-code published at github.com/alexandru/stuff-classifier.
2.1. General Algorithm #
You simply get the probability for a text to belong to each of the categories you test against. The category with the highest probability for the given text wins:
Do note that above I also eliminated the denominator from our original formula, because it is a constant that we do not need (called evidence).
2.2. Avoiding Floating Point Underflow (UPDATE Feb 27, 2012) #
Because of the underlying limits of floating points, if you’re working with big documents (not the case in this example), you do have to make one important optimization to the above formula:
- instead of the probabilities of each word, you store the (natural) logarithms of those probabilities
- instead of multiplying the numbers, you add them instead
So instead of the above formula, if you need this optimization, then use this one:
2.3. Training #
Your implementation must have a training method. Here’s how mine looks like:
def train(category, text)
each_word(text) {|w| increment_word(w, category) }
increment_cat(category)
end
And its usage:
classifier.train :spam, "Grow your penis to 20 inches in just 1 week"
classifier.train :ham, "I'm hungry, no I don't want your penis"
For the full implementation, take a look at base.rb.
2.4. Getting Rid of Stop Words / Stemming #
First of all, you must get rid of the junk. Every language has words that are so commonly used that make them meaningless for any kind of classification you may want to do. For instance in English you have words such as “the”, “to”, “you”, “he”, “only”, “if”, “it” that you can safely strip out from the text.
I’ve compiled a list of such words in this file: stop_words.rb. You can compile such a list by yourself if you’re not using English for example. Head over to Project Gutenberg, download some books in the language you want, count the words in them, sort by popularity in descending order and keep the top words as words that you can safely ignore.
Also, our classifier is really dumb in the sense that it does not care about the meaning or context of a word. So there’s a problem: consider the word “running”. What you want is to treat this just as “run”, which is the morphological root of the word. You also want to treat “parenting” and “parents” as “parent”.
This process is called stemming and there are lots of libraries for it. I think currently the most up-to-date and comprehensive library for stemming is Snowball. It’s a C library with lots of bindings available, including for Ruby and Python and it even has support for my native language (Romanian).
Take a look at what I’m doing in tokenizer.rb, where I’m getting rid of stop words and stemming the remaining.
each_word('Hello world! How are you?')
# => ["hello", "world"]
each_word('Lots of dogs, lots of cats!
This is the information highway')
# => ["lot", "dog", "lot", "cat", "inform", "highwai"]
each_word("I don't really get what you want to
accomplish. There is a class TestEval2, you can do test_eval2 =
TestEval2.new afterwards. And: class A ... end always yields nil, so
your output is ok I guess ;-)")
# => ["really", "want", "accomplish", "class",
# "testeval", "test", "eval", "testeval", "new",
# "class", "end", "yields", "nil", "output",
# "ok", "guess"]
NOTE: depending on the size of your training data, this may not be a good idea. Stemming is useful in the beginning when you don’t have a lot of data. Otherwise consider “house” and “housing” … the former is used less frequently in a spammy context then the later.
2.5. Implementation Guidelines #
When classifying emails for spam, it is a good idea to be sure that a certain message is a spam message, otherwise users may get pissed by too many false positives.
Therefore it is a good idea to have thresholds. This is how my implementation looks like:
def classify(text, default=nil)
# Find the category with the highest probability
max_prob = 0.0
best = nil
scores = cat_scores(text)
scores.each do |score|
cat, prob = score
if prob > max_prob
max_prob = prob
best = cat
end
end
# Return the default category in case the threshold condition was
# not met. For example, if the threshold for :spam is 1.2
#
# :spam => 0.73, :ham => 0.40 (OK)
# :spam => 0.80, :ham => 0.70 (Fail, :ham is too close)
return default unless best
threshold = @thresholds[best] || 1.0
scores.each do |score|
cat, prob = score
next if cat == best
return default if prob * threshold > max_prob
end
return best
end
Final Words #
My example involved spam classification, however this is not how modern spam classifiers work btw. Because the independence assumptions are often inaccurate, this type of classifier can be gamed by spammers to trigger a lot of false positives, which will make the user turn the feature off eventually.
But it is general purpose, being good enough not only for spam detection, but also for lots of other use-cases and it’s enough to get you started.